ATPS ETAPA 3 E 4

 Olá pessoal ! Vamos dar sequencia as nossas atividades práticas (ATPS) !

Vamos elaborar a Etapa 3 e 4, para nosso aprendizado e desenvolvimento em matemática! Vamos lá !

ATPS DE MATEMÁTICA ETAPA 3

PASSO 1

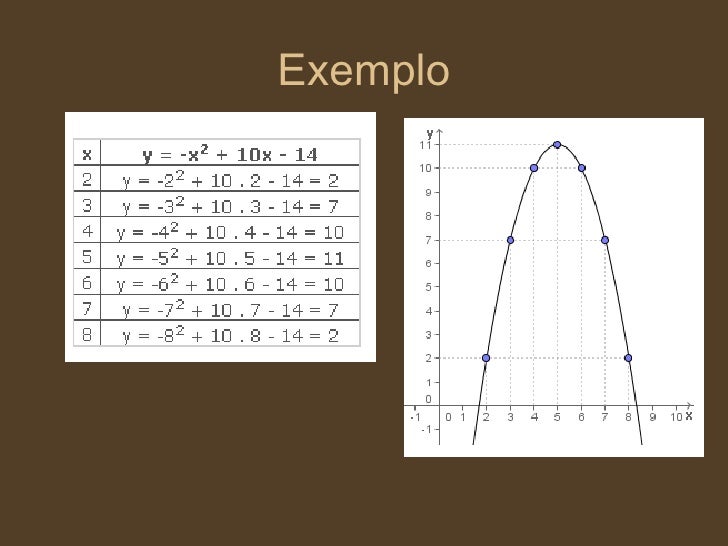
O lucro L obtido pela empresa na venda de um adubo específico é em função do preço x cobrado. Se x for um número muito pequeno, o lucro é negativo, ou seja, a empresa terá prejuízo. Se x for um número muito grande, o lucro também será negativo, pois poucas pessoas adquirirão o adubo dessa empresa. A matriz da empresa, estudando a situação, deduziu a fórmula para L em função de x: L = -x² + 90x– 1400. (L e x em unidades monetárias convenientes).

PASSO 2

1. Discutir e demonstrar por meio de cálculos se haverá lucro se o preço for x = 20 e se o preço for x = 70.

L(20) = -20² + 90.20 – 1400 = -400 + 1800 – 1400 = 0

L(70)= -70² + 90.70 – 1400 = -4900 + 6300 – 1400 = 0

Não haverá lucro nos dois, embora não haja prejuízos.

2. Explicar o que acontecerá quando x = 100. Esboçar o gráfico dessa função.

L(100) = -100² + 90.100 – 1400 = -10000 + 9000 – 1400 = -2400

O prejuízo será de 2400 reais

 PASSO 3

Definir quanto à empresa deverá cobrar (moeda vigente) para ter lucro máximo? Qual é esse lucro máximo?

O vértice dessa parábola representa o ponto de máximo da função, já que é uma parábola com a concavidade voltada para baixo, pois o coeficiente a é menor que zero (a = -1).

Se a função L = -x² + 90x – 1400

Temos os coeficientes: a = - 1, b= 90 e c= - 1400

Então

L(x) = -x² + 90x - 1400

L= -2x + 90L= 0
x= 45
A empresa obterá lucro máximo se comercializar ao preço de $45

Este lucro será:

L(45)= -45² + 90 . 45 – 1400 = -2025 + 4050 – 1400 = 625 A empresa obterá lucro máximo se comercializar ao preço de $45
Este lucro será:

L(45)= -45² + 90 . 45 – 1400 = -2025 + 4050 – 1400 = 625 
Este lucro será:
L(45)= -45² + 90 . 45 – 1400 = -2025 + 4050 – 1400 = 625 
L(45)= -45² + 90 . 45 – 1400 = -2025 + 4050 – 1400 = 625 

-2x + 90 = 0

ATPS DE MATEMÁTICA ETAPA 4

Passo 1 

Ler as informações relacionadas abaixo, para resolver as solicitações dos próximos passos.

Para todos os participantes do grêmio de funcionários é descontado 1% de seu salário mensal como contribuição. Dentre diversas vantagens o colaborador participante do grêmio tem acesso a empréstimos em um banco parceiro que ofereceu, para escolhas de sua equipe, duas opções de taxas:

1ª) Taxa de 4,4% ao mês, a juros simples.

2ª) Taxa de 1,75% ao mês, a juros compostos.

Outra excelente vantagem é uma bonificação anual aos motoristas de carretas, proporcional a 1,5% do valor atual dos veículos.

Passo 2

1. Definir uma função que descreva o montante a ser pago em função do tempo de empréstimo para cada modalidade oferecida e calcular, para um empréstimo de R$ 10.000,00 o montante a ser pago ao final de quatro meses em cada opção dada. Demonstrar, para quatro meses, em quantos reais os juros cobrados na melhor modalidade serão menores do que os cobrados na outra modalidade.

Opção 1

J = C.i.t             sendo  C = R$ 10.000,00

                                       I = 4,4%a.m = 0,044

                                       T = 4m

M = C + C.i.t

M = C (1 + it)

Então: M = 10000 (1 + 0,044.4)

M = 100000 (1,176)

M = R$ 11.760,00

Juros cobrados de R$ 1.760,00

Opção 2

A melhor modalidade é a 2ª opção (juros compostos de 1,75%a.m)

Os juros cobrados serão menores em R$ 1,041,00

2. Definir a melhor modalidade a ser escolhida em função do número de mesest no intervalos 1 < t < 42. Anotar todo o processo  de resolução e os resultados obtidos.

A melhor modalidade é a 2ª opção (juros compostos de 1,75% a.m)

Passo 3

Calcular o valor de bonificação total dada aos motoristas de carreta sabendo que cada carreta foi comprada há 3 anos por R$ 150.000,00 e que anualmente este equipamento sofre uma depreciação de 15,2%.

Bonificação anual dada aos motoristas de carretas, proporcional a 1,5% do valor atual dos veículos.

Calculo da bonificação

São 15 carretas, então 15 motoristas.

O valor de bonificação total dada aos motoristas de carreta é R$ 1,908.15 = R$ 28.620,00.

REVISÃO DE FUNÇÕES

Olá pessoal hoje estamos passando para darmos uma pequena revisada sobre o que é função, vamos lá!! 

A importância do estudo de função não é restrita apenas aos interesses da matemática, mas colocado em prática em outras ciências, como a física e a química.
Na matemática, o estudo de função é dividido basicamente em:

• Características, tipos e elementos de uma função.
• Função do primeiro grau.
• Função do segundo grau.

Nem sempre percebemos, mas estamos em contato com as funções no nosso dia a dia, por exemplo:

Quando assistimos ou lemos um jornal, muitas vezes nos deparamos com um gráfico, que nada mais é que uma relação, comparação de duas grandezas ou até mesmo uma função, mas representada graficamente.
Para que esse gráfico tome forma é necessário que essa relação, comparação, seja representada em uma função na forma algébrica.

Para dar início ao estudo de função é necessário o conhecimento de equações, pois todo o desenvolvimento algébrico de uma função é resolvido através de equações.

Canais de Funções

• 
  Função de 1º Grau
  Estudando a função de 1° grau através dos seus diversos elementos, como o cálculo do valor numérico da função e construção do gráfico de uma função do 1° grau.
• 
  Função de 2º Grau
  Função de 2º Grau, Gráfico da Função de 2º Grau, Inequação de 2º Grau, Máximo e Mínimo, Raizes da Função de 2º Grau, Sinais, O que é função de 2º Grau.

Na análise de fenômenos econômicos, muitas vezes usamos funções matemáticas para descre vê-los e interpretá-los.

Nesse sentido, as funções matemáticas são usa das como ferramentas que auxiliam na resolução de problemas ligados à administração de empresas. Nesta seção descrevemos o conceito de
função e algumas de suas representações.

Função crescente e decrescente

s funções que são expressas pela lei de formação y = ax + b ou f(x) = ax + b, onde a e b pertencem ao conjunto dos números reais, com a ≠ 0, são consideradas funções do 1º grau. Esse tipo de função pode ser classificada de acordo com o valor do coeficiente a, se a > 0, a função é crescente, caso a < 0, a função se torna decrescente.

Vamos analisar as seguintes funções f(x) = 3x e f(x) = –3x, com domínio no conjunto dos números reais, na medida em que os valores de x aumentam.

Tipos de função

Função é um dos conceitos mais importantes da matemática. Existem várias definições, dependendo da forma como são escolhidos os axiomas. Uma relação entre dois conjuntos, onde há uma relação entre cada um de seus elementos. Também pode ser uma lei que para cada valor x é correspondido por um elemento y, também denotado por ƒ(x). Existem inúmeros tipos de funções matemáticas, entre as principais temos: função sobrejetora, função injetora, função bijetora, função trigonométrica, função linear, função modular, função quadrática, função exponencial, função logarítmica, função polinomial, dentre inúmeras outras. Cada função é definida por leis generalizadas e propriedades específicas

• Aplicações de uma Função Exponencial
  Exemplos de aplicação de uma função exponencial.
• Área sob uma Curva
  Determinando a área de uma região através do cálculo da Integral.
• Como construir o gráfico de uma função?
  Aprenda os passos para construir o gráfico de uma função e aplique para qualquer tipo de função!
• Composição de três ou mais funções
  Dúvidas ao resolver a composição de três ou mais funções? Então confira nossas dicas e veja a resolução comentada de alguns exemplos!
• Coordenadas de Localização Absoluta
  Localização de pontos na esfera terrestre.
• Fórmulas Fundamentais de Integração
  Conheça as fórmulas para a integração de funções.
• Função
  O estudo das funções se apresenta em vários segmentos. Clique e entenda!
• Função Composta
  Conheça a composição de uma função.
• Função definida por fórmula
  Leis de formação de funções.
• Função Exponencial
  Propriedades e características de uma função exponencial.
• Função inversa
  Determinando a função inversa.
• Função Logarítmica
  Estudo da Função Logarítmica.
• Função modular
  Definição e gráficos da função modular
• Função Par e Função Ímpar
  Saiba identificar uma função par ou ímpar.
• Função Polinomial
  Conheça a definição e as propriedades de uma função polinomial. Clique aqui!
• Função quadrática na forma canônica
  Determinando a forma canônica da função quadrática através da manipulação algébrica. Expressão canônica da função quadrática.
• Funções e Matemática Financeira
  Gráficos: juros simples e compostos.
• Funções periódicas
  Definição das funções periódicas e alguns exemplos. Compreendendo e definindo as funções periódicas e estudando o período de funções desse tipo.
• Inequação Produto e Inequação Quociente
  Estudo das Inequações.
• Inequações modulares
  Definição e propriedades de uma inequação modular.
• Introdução à Função
  Estudos introdutórios envolvendo função.
• Limite de uma Função
  Noção de Limite.
• Matemática na Economia: Função Custo, Função Receita e Função Lucro
  funções custo, receita e lucro.
• Máximo e Mínimo da função na forma canônica
  Analisando os coeficientes da função quadrática canônica para determinar os valores de máximo e mínimo. Obtendo os valores de máximo e mínimo de uma função quadrática.
• Pontos de Nivelamento
  Pontos críticos da função lucro.
• Propriedades de uma função
  Função, Característica de função, Função sobrejetora, Função injetora, Função bijetora, Imagem de uma função, imagem, imagem de uma função, contra domínio, Contra domínio de uma função.
• Relação
  Conceito de relação, Gráficos que representam uma relação, Gráfico que representa uma função, Domínio de uma relação, Imagem de uma relação, Forma de escrever uma relação, Par ordenado, Representação gráfica, Representação de uma relação através de uma re
• Representação Gráfica de Funções
  Funções e suas representações gráficas.
• Taxa de Variação da Função do 2º Grau
  Inclinação da reta tangente à parábola.
• Tipos de Função
  Propriedades e definição dos tipos de função.
• espero que tenham  gostado ate logo pessoal!

FUNÇÃO DO 2º GRAU

Olá pessoal hoje veremos um pouco sobre função de 2º grau, assim vocês poderam entender melhor a nossa 2 etapa da ATPS ...


DEFINIÇÃO

 Toda função é estabelecida pela lei de formção
           f(x) = ax² + bx + c 
    
 Com A, B e C números reais e a≠0, é denominada função de 2º grau.




GRÁFICO 

 A Representação geométrica de uma funçãp do 2º grau é dada por uma parábola, que de acordo com a sinal do coeficiente A pode ter concavidade voltada para cima ou para baixo
   
     Coeficiente A > 0, Parábola com a concavidade voltada para cima

     Coeficiente A < 0, Parábola com a concavidade voltada para baixo











ESTUDO DO GRÁFICO DE UMA FUNÇÃO DE 2º GRAU

 Raizes de uma função do 2º frau 
  As raizes de uma função do 2º grau são dadas quando fazemos y ou f (x) igual a zero, ou seja , quando calcularmos  f(x)=0  encontramos os pontos onde a função passa pelo eixo X

Para encontrar em quais pontos a função cruza o eixo x, formatamos a função como uma equação do 2º grau, encontrando as suas raízes, utilizando o teorema de Bháskara

PASSO A PASSO PARA TRAÇAR O GRÁFICO DA FUNÇÃO DE 2º GRAU

1º  Verifiquer de o coeficiente  a<0 ou a>0 , parábola voltada para cima ou para baixo.

2º Igular a função a zero e encontrar a raízes da função( onde corta o eixo x).

3º Encontrar as coordenadas do vértice da função (utilizando a formula